PadaKumpulan Topik Materi Trigonometri (Dengan Bahasan Lengkap) – Trigonometri mempunyai asal kata dari bahasa Yunani yaitu “trigonon” yang berarti tiga sudut dengan “metron” yang berarti mengukur.
Trigonometri adalah cabang dari ilmu matematika yang di dalamnya membahas tentang hubungan panjang dan sudut segitiga. Trigonometri mulai ada di abag 3 SM pada masa hellenistik untuk mempelajari ilmu astronomi.
Kumpulan Topik Materi Trigonometri (Dengan Bahasan Lengkap)
Di abad ke 3 SM, astronom untuk pertamak kalinya mencatat panjang sudut-sudut dan sisi-sisi segitiga siku-siku. Dan tiap-tiap sisi mempunyai hubungan apabila minimal salah satu nilai sudut dan panjang sisi diketahui, maka semua panjang sisi dan nilai sudut bisa ditentukan menggunakan algoritme.
Perhitungan tersebut diartikan sebagai fungsi trigonometri dan telah menjadi bagian dari matematika murni maupun terapan, sebagai contoh untuk menganalisis metode dasar (gelombang persamaan, transformasi fourier, dan lain-lain), memahami fenomena fisika, teknik kelistrikan dan mesin, biologi bahkan musik dan akustik. Selain itu, trigonometri juga mempunyai peran dalam menemukan survey.
Dalam perancangan kerangka jembatan perhitungan yang digunakan tentu sangat rumit meliputi tegangan sampai gaya yang bekerja pada jembatan tersebut adalah fokus utama perancang jembatan dalam membuat konstruksi model rancangan.
Proses perancangan itu harus berdasarkan pengetahuan bangsa Romawi yakni busur mampu menjangkau jarak yang lebih jauh serta menahan beban yang lebih berat dibandingkan bentuk balok lurus horizontal (lintel).
Dasar tersebut dipakai untuk membangun jembatan busur yang meliputi kelengkungan yang wajib diperhitungkan kemiringan sudutnya yang menggunakan persamaan trigonometri.
Fungsi Trigonometri
Trigonometri adalah ilmu khusus yang membahas segitiga siku-siku segitiga atau siku segitiga. Matematikan dalam trigonometri memiliki tiga fungsi yaitu :
- Sinus (sin) adalah perbandingan sisi segitiga di mana segitiga siku-siku atau dalah satu sudut segitiga adalah 90o yang berada di depan sudut sisi miring.
- Kosinus (cos) perbandingan sisi segitiga yang berada di sisi miring.
- Tangen (tan) adalah perbandingan sisi segitiga yang berada di depan sudur dan sisi segitiga yang ada di sudut.

Hal yang harus dilakukan lebih dulu sebelum mempelajari tiga fungsi tersebut lebih lanjut adalah memahami konsep dasar segitiga terlebih segitiga siku-siku. Segitiga memiliki sisi 3 buah yakni sisi samping, sisi depan dan sisi miring.
Segitiga juga mempunyai tiga sudut yakni sudut depan, sudut tegak lurus dan sudut samping yang apabila sudut-sudut itu dijumlahkan maka nilainya 180o.
Konsep Trigonometri Dasar
Pembahasan dalam konsep trigonometri dasar adalah trigonometri penjabaran sisi segitiga dengan istilah-istilah yang umum digunakan dan rumus trigonometri dasar. Selain itu, akan dipelajari juga mengeai konsep penggunaan rumus dasar, misalnya cosecan, cotangen dan sinus.
Bab-bab lain yang termasuk pembahasan trogonometri adalah sudut lebih dari 360o, perbandingan sudut istimewa, perbandingan sudut berelasi di kuadran I, koordinat kutub dan perbandingan sudut negatif.
Identitas dan Persamaan Trigonometri
Sesudah memahami konsep trigonometri dasar, maka materi selanjutnya yang akan diberikan adalah identitas dan persamaan trigonometri. Identitas trigonometri ialah sebuah operasi yang dilakukan dalam membuktikan dua pernyataan ekuivalen atau mengubah bentuk sebuah pernyataan. Persamaan trigonometri yaitu suatu persamaan yang mempunyai satu bahkan lebih fungsi trigonometri.
Ada korelasi antara persamaan dan identitas trigonometri sehingga dibutuhkan prinsip identitas guna menyederhanakan persamaan menjadi bentuk paling sederhana dalam menuntaskan persamaan trigonometri. Cara lainnya yang bisa digunakan untuk menyederhanakan persamaan yaitu memakai aljabar.
Pada Persamaan 1
![]()
Persamaan 2
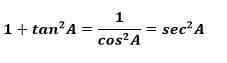
Dan Persamaan 3
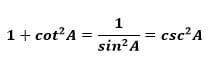
Konsep Sinus, Cosinus dan Luas Segitiga
Sebagaimana sudah dijelaskan sebelumnya mengenai pemahaman sifat-sifat dasar beserta rumus-rumus dasar segitiga yang akan sangat membantu dalam menguasai konsep sinus, cosinus dan luas segitiga ini. penjelasan ini adalah seputar aturan-aturan sinus dan cosinus yang dapat diterapkan dalam segitiga.
Ada aturan sinus yang bisa dipakai apabila ada dua sudut yang satu sisinya diketahui atau dua sisi dan satu sudut segitiga diketahui. Aturan cosinus yang bisa diterapkan jika panjang sisi-sisi segitiga serta cosinus salah satu sudut segitiga diketahui.
Selain dengan dua cara di atas, luas segitiga juga bisa dicari apabila salah satu sudut diketahui sinusnya. Rumus-rumus di bawah ini wajib dikuasai dalam mengerjakan soal-soal.
Rumus 1
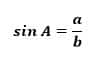
Lalu Rumus 2
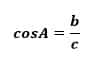
Rumus 3
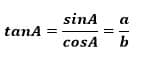
Lalu Rumus 4
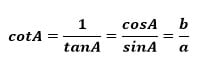
Rumus 5
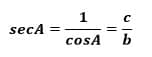
Dan Rumus 6
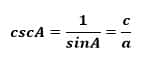
Konsep Trigonometri dengan Jumlah Dua Sudut
Konsep trigonometri dengan jumlah dua sudut bisa dipakai dalam menghitung sudut-sudut yang mempunyai besaran di dalamnya ada sudut istimewa, seperti sudut 18o. Dengan memakai konsep trigonometri dengan jumlah dua sudut akan mempermudah penghitungan sinus, cosinus dan tangen sudut-sudut itu.
Penggunaan konsep trigonometri dengan jumlah dua sudut pun bisa diterapkan dalam membuktikan besaran sudut yang sudah diketahui. Materi-materi yang akan dipelajari dalam kesempatan ini misalnya penjumlahan dan pengurangan dua sudut sinus, penjumlahan dan pengurangan dua sudut cosinus, tangen dan sudut rangkap.
Konsep Operasi Fungsi Trigonometri
Bahasan selanjunya yaitu konsep operasi fungsi trigonometri. Operasi fungsi trigonometri merupakan suatu operasi dasar yang penerapannya meliputi fungsi-fungsi dasar trigonometri. Secara mendasar, operrasi fungsi dasar trigonometri adalah operasi yang dipakai untuk menyederhanakan sebuah pernyataan sehingga akan lebih mudah untuk dihitung secara matematika.
Pada pembahasan ini pun diberikan penjelasan tentang pembuktian hasil penjumlahan, pengurangan dan perkalian fungsi.
Oleh sebab itu, materi-materi yang akan disampaikan dalam materi trigonometri berupa penjumlahan fungsi, pengurangan fungsi dan perkalian fungsi. Penguasaan konsep materi trigonometri benar-benar dibutuhkan supaya bisa mempelajari materi ini lebih lanjut.
Banyak contoh soal terkait materi trigonometri dan penyertaan pembahasan tiap-tiap konsep trigonometri bisa membantu dalam penyelesaian soal-soal konsep trigonometri tersebut.
Itulah penjelasan materi Kumpulan Topik Materi Trigonometri (Dengan Bahasan Lengkap). Semoga penjelasan di atas bisa menambah pemahaman para pembaca tentang konsep-konsep trigonometri 🙂
